HABILIDADE 9

02. H9 (Enem 2019) Um aplicativo de relacionamentos funciona da seguinte forma: o usuário cria um perfil com foto e informações pessoais, indica as características dos usuários com quem deseja estabelecer contato e determina um raio de abrangência a partir da sua localização. O aplicativo identifica as pessoas que se encaixam no perfil desejado e que estão a uma distância do usuário menor ou igual ao raio de abrangência. Caso dois usuários tenham perfis compatíveis e estejam numa região de abrangência comum a ambos, o aplicativo promove o contato entre os usuários, o que é chamado de match.

O usuário P define um raio de abrangência com medida de   e busca ampliar a possibilidade de obter um match se deslocando para a região central da cidade, que concentra um maior número de usuários. O gráfico ilustra alguns bares que o usuário P costuma frequentar para ativar o aplicativo, indicados por I, II, III, IV e V. Sabe-se que os usuários Q, R e S, cujas posições estão descritas pelo gráfico, são compatíveis com o usuário P, e que estes definiram raios de abrangência respectivamente iguais a 3 km, 2 km e 5 km.

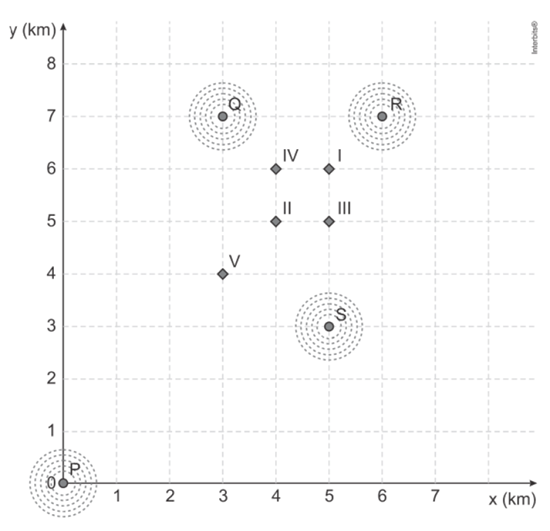
Com base no gráfico e nas afirmações anteriores, em qual bar o usuário P teria a possibilidade de um match com os usuários Q, R e S, simultaneamente?

03. H9 (Enem 2018)  Minecraft é um jogo virtual que pode auxiliar no desenvolvimento de conhecimentos relacionados a espaço e forma. É possível criar casas, edifícios, monumentos e até naves espaciais, tudo em escala real, através do empilhamento de cubinhos.

Um jogador deseja construir um cubo com dimensões

4  x 4 x 4. Ele já empilhou alguns dos cubinhos necessários, conforme a figura.

Os cubinhos que ainda faltam empilhar para finalizar a construção do cubo, juntos, formam uma peça única, capaz de completar a tarefa.

O formato da peça capaz de completar o cubo 4 x 4 x 4 é

04. H9 (Enem 2017) A imagem apresentada na figura é uma cópia em preto e branco da tela quadrada intitulada O peixe, de Marcos Pinto, que foi colocada em uma parede para exposição e fixada nos pontos A e B.

Por um problema na fixação de um dos pontos, a tela se desprendeu, girando rente à parede. Após o giro, ela ficou posicionada como ilustrado na figura, formando um ângulo de 45° com a linha do horizonte.

Para recolocar a tela na sua posição original, deve-se girá-la, rente à parede, no menor ângulo possível inferior a 360°.

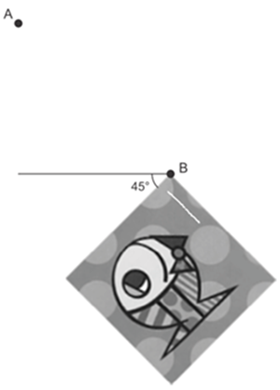
A forma de recolocar a tela na posição original, obedecendo ao que foi estabelecido, é girando-a em um ângulo de

05. H9 (Enem 2017) Uma desenhista projetista deverá desenhar uma tampa de panela em forma circular. Para realizar esse desenho, ela dispõe, no momento, de apenas um compasso, cujo comprimento das hastes é de 10 cm, um transferidor e uma folha de papel com um plano cartesiano. Para esboçar o desenho dessa tampa, ela afastou as hastes do compasso de forma que o ângulo formado por elas fosse de 120°. A ponta seca está representada pelo ponto C, a ponta do grafite está representada pelo ponto B e a cabeça do compasso está representada pelo ponto A  conforme a figura.

Após concluir o desenho, ela o encaminha para o setor de produção. Ao receber o desenho com a indicação do raio da tampa, verificará em qual intervalo este se encontra e decidirá o tipo de material a ser utilizado na sua fabricação, de acordo com os dados.

Considere 1,7 como aproximação para √3.

O tipo de material a ser utilizado pelo setor de produção será

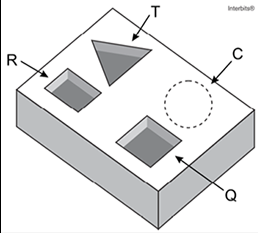
06. H9 (Enem 2016) Um marceneiro está construindo um material didático que corresponde ao encaixe de peças de madeira com de altura e formas geométricas variadas, num bloco de madeira em que cada peça se posicione na perfuração com seu formato correspondente, conforme ilustra a figura. O bloco de madeira já possui três perfurações prontas de bases distintas: uma quadrada (Q), de lado 4 cm, uma retangular (R), com base 3 cm e altura 4 cm, e uma em forma de um triângulo equilátero (T), de lado 6,8 cm. Falta realizar uma perfuração de base circular (C).

O marceneiro não quer que as outras peças caibam na perfuração circular e nem que a peça de base circular caiba nas demais perfurações e, para isso, escolherá o diâmetro do círculo que atenda a tais condições. Procurou em suas ferramentas uma serra copo (broca com formato circular) para perfurar a base em madeira, encontrando cinco exemplares, com diferentes medidas de diâmetros, como segue: (l) 3,8cm; (II) 4,7cm; (III) 5,6cm; (IV) 7,2cm e (V) 9,4cm.

Considere 1,4 e 1,7 como aproximações para √2 e √3, respectivamente.

Para que seja atingido o seu objetivo, qual dos exemplares de serra copo o marceneiro deverá escolher?

07. H9 (Enem 2015) O tampo de vidro de uma mesa quebrou-se e deverá ser substituído por outro que tenha a forma de círculo. O suporte de apoio da mesa tem o formato de um prisma reto, de base em forma de triângulo equilátero com lados medindo 30 cm.

Uma loja comercializa cinco tipos de tampos de vidro circulares com cortes já padronizados, cujos raios medem 18 cm, 26 cm, 30 cm, 35 cm e 60 cm. O proprietário da mesa deseja adquirir nessa loja o tampo de menor diâmetro que seja suficiente para cobrir a base superior do suporte da mesa.

Considere 1,7 como aproximação para √3.

O tampo a ser escolhido será aquele cujo raio, em centímetros, é igual a

08. H9 (Enem 2015) Para uma alimentação saudável, recomenda-se ingerir, em relação ao total de calorias diárias, 60% de carboidratos, 10% de proteínas e 30% de gorduras. Uma nutricionista, para melhorar a visualização dessas porcentagens, quer dispor esses dados em um polígono. Ela pode fazer isso em um triângulo equilátero, um losango, um pentágono regular, um hexágono regular ou um octógono regular, desde que o polígono seja dividido em regiões cujas áreas sejam proporcionais às porcentagens mencionadas. Ela desenhou as seguintes figuras:

Entre esses polígonos, o único que satisfaz as condições necessárias para representar a ingestão correta de diferentes tipos de alimentos é o

09. H9 (Enem 2014)  Conforme regulamento da Agência Nacional de Aviação Civil (Anac), o passageiro que embarcar em voo doméstico poderá transportar bagagem de mão, contudo a soma das dimensões da bagagem (altura + comprimento + largura) não pode ser superior a 115cm.

A figura mostra a planificação de uma caixa que tem a forma de um paralelepípedo retângulo.

O maior valor possível para x, em centímetros, para que a caixa permaneça dentro dos padrões permitidos pela Anac é

10. H9 (Enem 2013) Um restaurante utiliza, para servir bebidas, bandejas com base quadradas. Todos os copos desse restaurante têm o formato representado na figura:

Considere que \(\overline{AC}=\frac{7}{5}\overline{BD}\) e que \(\ell\) é a medida de um dos lados da base da bandeja.

Qual deve ser o menor valor da razão \(\frac{\underline{\ell}}{BD}\) para que uma bandeja tenha capacidade de portar exatamente quatro copos de uma só vez?

11. H9 (Enem 2013) As torres Puerta de Europa são duas torres inclinadas uma contra a outra, construídas numa avenida de Madri, na Espanha. A inclinação das torres é de 15° com a vertical e elas têm, cada uma, uma altura de 114 m (a altura é indicada na figura como o segmento AB). Estas torres são um bom exemplo de um prisma oblíquo de base quadrada e uma delas pode ser observada na imagem.

Utilizando 0,26 como valor aproximado para tangente de 15° e duas casas decimais nas operações, descobre-se que a área da base desse prédio ocupa na avenida um espaço

12. H9 (Enem 2012) Em exposições de artes plásticas, é usual que estátuas sejam expostas sobre plataformas giratórias. Uma medida de segurança é que a base da escultura esteja integralmente apoiada sobre a plataforma. Para que se providencie o equipamento adequado, no caso de uma base quadrada que será fixada sobre uma plataforma circular, o auxiliar técnico do evento deve estimar a medida R do raio adequado para a plataforma em termos da medida L do lado da base da estatua.

Qual relação entre R e L o auxiliar técnico deverá apresentar de modo que a exigência de segurança seja cumprida?‍

13. H9 (Enem 2011) O atletismo é um dos esportes que mais se identificam com o espírito olímpico. A figura ilustra uma pista de atletismo. A pista é composta por oito raias e tem largura de 9,76 m. As raias são numeradas do centro da pista para a extremidade e são construídas de segmentos de retas paralelas e arcos de circunferência. Os dois semicírculos da pista são iguais.

‍‍

Se os atletas partissem do mesmo ponto, dando uma volta completa, em qual das raias o corredor estaria sendo beneficiado?‍

14. H9 (Enem 2010) Uma metalúrgica recebeu uma encomenda para fabricar, em grande quantidade, uma peça com o formato de um prisma reto com base triangular, cujas dimensões da base são 6 cm, 8 cm e 10 cm e cuja altura é 10 cm. Tal peça deve ser vazada de tal maneira que a perfuração na forma de um cilindro circular reto seja tangente as suas faces laterais, conforme mostra a figura.‍

O raio da perfuração da peça é igual a

15. H9 (Enem 2010)  Dona Maria, diarista na casa da família Teixeira, precisa fazer café para servir as vinte pessoas que se encontram numa reunião na sala. Para fazer o café, Dona Maria dispõe de uma leiteira cilíndrica e copinhos plásticos, também cilíndricos.

Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade mínima de água na leiteira para encher os vinte copinhos pela metade. Para que isso ocorra, Dona Maria deverá